Note that since the text and image below were created we have switched to using quadsphere level-6 bins for searches. Each level-6 bin covers the same area as 4 level-7 bins.
The specification of geographical areas of interest in the ocean color browser is done in terms of equal area bins defined using the quad-sphere binning scheme at level 7. These bins are roughly 72 kilometers across.
The example image below has been marked with the quad-sphere,
level-7 bin boundaries to give you a better idea of their
size.

Some programs that search for satellite data granules implement
their geographical searches in terms of corner coordinates or
coordinate extrema (i.e. maximum and minimum latitude and longitude).
Such searches will often yield more "false positive"
results than this interface. The reason for this is explained
by the image below. (Clicking on the image will download a larger version.)
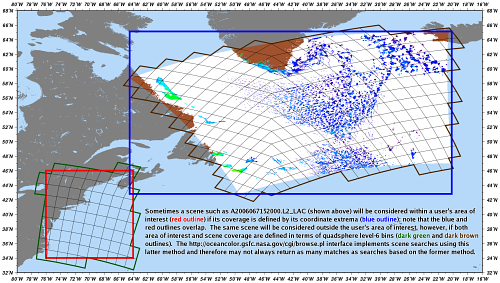
Sometimes a scene such as A2006067152000.L2_LAC (shown above)
will be considered within a user's area of interest (red outline)
if its coverage is defined by its coordinate extrema (blue outline);
note that the blue and red outlines overlap. The same scene will
be considered outside the user's area of interest, however, if both
area of interest and scene coverage are defined in terms of quadsphere
level-6 bins (dark green and dark brown outlines). The
https://oceancolor.gsfc.nasa.gov/cgi/browse.pl interface implements
scene searches using this latter method and therefore may not always
return as many matches as searches based on the former method.
A more formal definition of the quad-sphere binning scheme follows.
ROUTINE TO COMPUTE QUAD-SPHERE BIN NUMBER
FROM LATITUDE AND LONGITUDE
Program logic generated by:
Frederick S. Patt / General Sciences Corporation
March 6, 1992
Quad Sphere
The Earth's surface is projected onto the faces of an inscribed cube using
a curvilinear projection which preserves area. The sphere is divided into
six equal areas which correspond to the faces of the cube. The vertices of
the cube correspond to the cartesian coordinates defined by |x|=|y|=|z| on
the unit sphere. The cube is oriented with one face normal to the North
Pole and one face centered on the Greenwich meridian.
The faces of the cube are divided into square bins, where the number of
bins along each edge is a power of 2, selected to produce the desired bin
size. Thus the number of bins on each face is 2**(2*N), where N is the
binning level, and the total number of bins is 6*2**(2*N). For example, a
level of 10 gives 1024x1024 bins on each face and 6291456 (6*2**20) total
bins, and on the Earth's surface the bins are 81 km**2 in size.
The bins are numbered serially, and the bin numbers are determined as
follows. The total number of bits required for the bin numbers at level N
is 2*N+3, where the 3 MSBs are used for the face numbers and the remaining
bits are used to number the bins within each face. The faces are numbered
0-5 with 0 being the North face, 1 through 4 being equatorial with 1
corresponding to Greenwich, and 5 being South. Thus at level 10, face 0
has bin numbers 0-1048575, face 1 has numbers 1048576-2097151, etc.
Within each face the bins are numbered serially from one corner (the
convention is to start at the "lower left") to the opposite corner, with
the ordering such that each pair of bits corresponds to a level of bin
resolution. This ordering in effect is a two-dimensional binary tree,
which is referred to as the quad-tree The conversion between bin numbers
and coordinates is straightforward. The maximum practical bin level is 14,
which uses 31 bits in a 32-bit integer and results in a bin size of 0.32
km**2.
The quad sphere limits the allowable bin sizes by requiring the bin
dimenension of the cube face to be a power of 2, due to the binary indexing
scheme. The advantage is that the bin numbering allows the resolution to
be changed (by factors of two) simply by adding or deleting LSBs. This is
particularly useful if it is desired to increase the bin size, for example
to compare maps with different resolutions. This is performed simply by
dividing the bin numbers by four for each factor of two increase in bin
size.
The quad sphere faces can be displayed individually without remapping, with
moderate distortion in the corners of the faces.
The quad sphere has an advantage in that the binary numbering scheme allows
contiguous subsets of bins (either whole faces or quadrants of faces) to be
accessed by simply specifying a range of bin numbers.
High-Level Logic:
1. Compute cartisian coordinates from LAT and LON
2. Determine face number and select coordinates for projection
3. Compute face coordinates (u,v) from cartesian coordinates
4. Compute pixel number from face coordinates using level number
Detailed Logic:
1. COMPUTE CARTESIAN COORDINATES (X,Y,Z) FROM LAT AND LON
X = COS(LAT)*COS(LON)
Y = COS(LAT)*SIN(LON)
Z = SIN(LAT)
2. DETERMINE FACE NUMBER AND SELECT COORDINATES (Q,R,S) FOR
PROJECTION; FACES ARE NUMBERD SUCH THAT Z AXIS IS NORMAL TO
FACE 0 AND X AXIS IS NORMAL TO FACE 1; PROJECTION COORDINATES
ARE CHOSEN SUCH THAT Q IS NORMAL TO CUBE FACE.
IF ((ABS(Z).GE.ABS(X)).AND.((ABS(Z).GE.ABS(Y)) THEN
IF (Z.GT.0.) THEN
IFACE = 0
Q = Z
R = Y
S = -X
ELSE
IFACE = 5
Q = -Z
R = Y
S = X
ELSE IF (ABS(X).GE.ABS(Y) THEN
IF (X.GT.0.) THEN
IFACE = 1
Q = X
R = Y
S = Z
ELSE
IFACE = 3
Q = -X
R = -Y
S = Z
ELSE
IF (Y.GT.0.) THEN
IFACE = 2
Q = Y
R = -X
S = Z
ELSE
IFACE = 4
Q = -Y
R = X
S = Z
END IF
3. COMPUTE FACE COORDINATES (U,V) FROM CARTESIAN COORDINATES
PROJECTION EQUATIONS ASSUME KNOWLEDGE OF LARGER OF (R,S)
IF (ABS(R).GE.ABS(S)) THEN
COMPUTE (U,V) FROM (Q,R,S)
U = SQRT((1.-Q)/(1.-1./SQRT(2.+(S/R)**2)))
V = U*(12./PI)*(ATAN(S/ABS(R))-ASIN(S/SQRT(2.*(R*R+S*S))))
U = U*SIGN(R)
ELSE
COMPUTE (V,U) FROM (Q,S,R)
V = SQRT((1.-Q)/(1.-1./SQRT(2.+(R/S)**2)))
U = V*(12./PI)*(ATAN(R/ABS(S))-ASIN(R/SQRT(2.*(R*R+S*S))))
V = V*SIGN(S)
END IF
4. COMPUTE PIXEL NUMBER FROM FACE COORDINATES USING LEVEL NUMBER
Convert (U,V) from range of (-1,+1) to (0,2**LEV-1)
IU = 2**LEV*(U+1.)/2.
IV = 2**LEV*(V+1.)/2.
Perform edge check to protect against invalid bin numbers
IF (IU.GE.2**LEV) IU = 2**LEV - 1
IF (IV.GE.2**LEV) IV = 2**LEV - 1
IF (IU.LT.0) IU = 0
IF (IV.LT.0) IV = 0
Use lookup table to convert indices (IU,IV) to bin number on face
Note that table array is used twice (for low and high bits)
IU1 = IU/128
IU2 = IU - IU1*128
IV1 = IV/128
IV2 = IV - IV1*128
BIN = TAB(IU1)*16384 + TAB(IU2) + TAB(IV1)*32768 + TAB(IV2)*2
Add face number as high order bits
BIN = BIN + IFACE*2**(2*LEV)
END DETAILED LOGIC
INCLUDE ARRAY TAB(128) USED BY PROGRAM FOR BIN NUMBER COMPUTATION
The entries in this table are generated by taking the binary
representations of integers 0 to 127 and inserting an extra 0 bit
between each pair of binary bits. This allows the U and V
coordinate indicies to be merged into a single bin number by
multiplying the V index by 2 and adding them together. Note that
array elements whose index is a power of 2 are equal to the index
squared. Thus,
TAB(0) = 0
TAB(1) = 1
TAB(2) = 4
TAB(3) = 5
TAB(4) = 16
TAB(5) = 17
TAB(6) = 20
TAB(7) = 21
TAB(8) = 64
.
.
.
TAB(125) = 5457
TAB(126) = 5460
TAB(127) = 5461
END INCLUDE