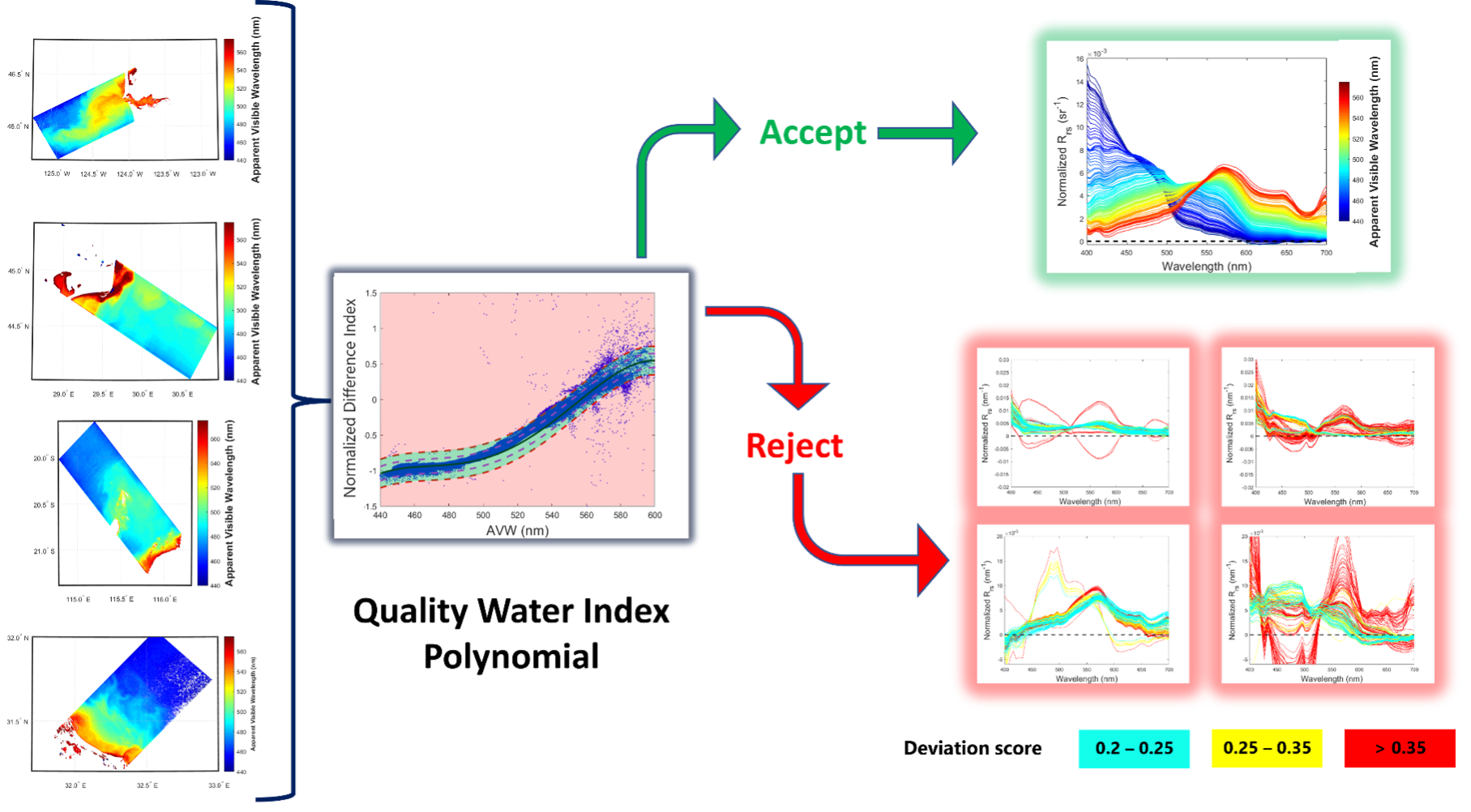
This algorithm returns the Quality Water Index Polynomial (QWIP) score, representing a quantitative metric to evaluate the quality of ocean color remote sensing reflectance ($R_{rs}$) data (Dierssen et al. 2022). The relationship between the Apparent Visible Wavelength (AVW; Vandermeulen et al. 2020) and a multi-channel waveband index is used to identify spectra that fall outside the general trends observed in aquatic optics for optically deep waters. The approach was developed with a large global dataset representing blue, green, and brown waters and was further tested extensively with field and satellite datasets. This simple approach can provide a level of uncertainty about a retrieved spectrum and flag questionable or unusual spectra for further analysis.

Algorithm Point of Contact: Heidi Dierssen, University of Connecticut
Inputs: $R_{rs}$ at all available wavelengths between 400 – 700 nm (rrs_vvv).
Outputs: qwip, Quality Water Index Polynomial score (unitless)
Approach: The Quality Water Index Polynomial (QWIP) is a mathematical model relating the calibrated Apparent Visible Wavelength (AVW, Vandermeulen et al. 2020) to a normalized difference index (NDI). The QWIP score is calculated as the difference between a measured and AVW-predicted NDI. To initiate, the measured NDI is determined as:
$$NDI = \frac{R_{rs} (\lambda_2) - R_{rs} (\lambda_1)}{R_{rs}(\lambda_2) + R_{rs} (\lambda_1)}$$where $\lambda1$ = Rrs_490, and $\lambda2$ = Rrs_665 (for multispectral sensors, the closest wavelength match is used).
The predicted NDI is related to the Apparent Visible Wavelength (AVW) as follows:
$$NDI_{predicted}=p_1AVW^{4}+p_2 AVW^{3}+p_3 AVW^{2}+p_4 AVW+p_5$$ $$p=(-8.399885\times10^{-9},1.715532 \times10^{-5},-1.301670 \times 10^{-2},4.357838 \times 10^{0},-5.449532 \times 10^{2} )$$Finally, the QWIP score is calculated as the difference between the NDI and NDI_predicted:
$$QWIP_{Score}=NDI(490,665)-NDI_{predicted}$$The NDI provides a means to highlight the variability of logarithmically distributed data on a linear scale such that the distance either above or below the central tendency (QWIP) can be scored with a positive or negative value. Generally, hyperspectral data with QWIP scores exceeding a value of |0.2| may be subject to additional screening to determine any evident spectral anomalies. It maybe necessary to relax the nominal threshold (e.g. |0.3|) when applying QWIP to multispectral sensors.
Product Short Name:
qwip
Level-2 Product Suite: None
Calling in L2GEN:
l2prod = qwip
qwip_coef = [p1,p2,p3,p4,p5]
Algorithm Development: The method was developed using a large global dataset of remote sensing reflectance (n = 1,629) compiled from different studies (CASCK-P dataset, see Dierssen et al. 2022).
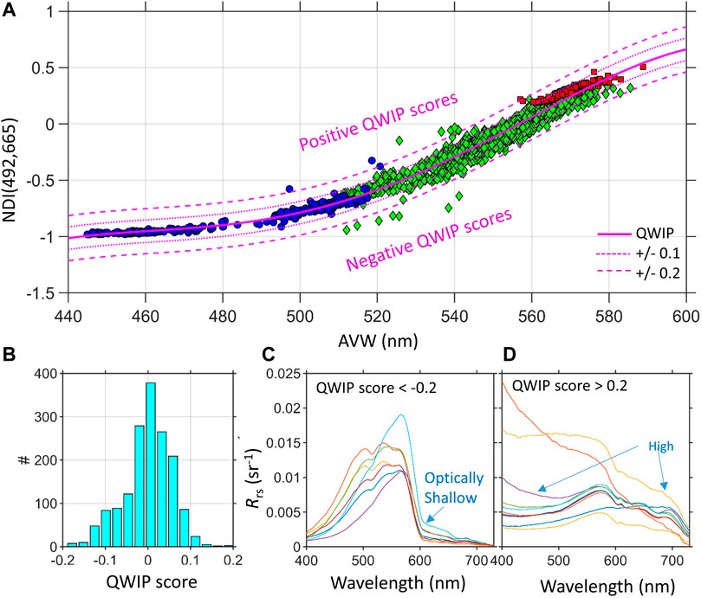
Algorithm Verification: The QWIP approach was tested using several different regional field datasets collected with above-water methodology and on satellite-retrievals of water-leaving reflectance data.
In situ verification:

In situ verification:
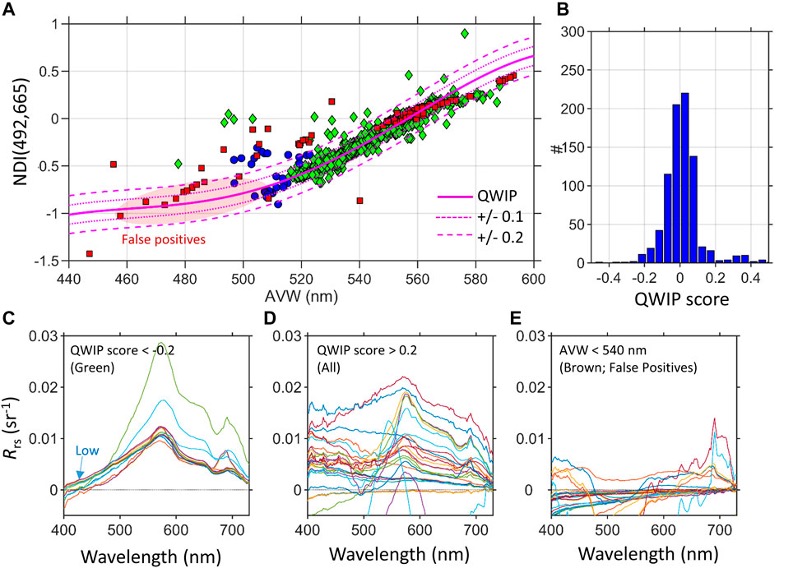
Satellite verification:
Dierssen, H. M., Vandermeulen, R. A., Barnes, B. B., Castagna, A., Knaeps, E., & Vanhellemont, Q., 2022: “QWIP: A Quantitative Metric for Quality Control of Aquatic Reflectance Spectral Shape using the Apparent Visible Wavelength,” Frontiers in Remote Sensing, 32. https://doi.org/10.3389/frsen.2022.869611
Vandermeulen, R. A., Mannino, A., Craig, S.E., Werdell, P.J., 2020: “150 shades of green: Using the full spectrum of remote sensing reflectance to elucidate color shifts in the ocean,” Remote Sensing of Environment, 247, 111900, https://doi.org/10.1016/j.rse.2020.111900
Vanhellemont, Q., 2020: “Sensitivity analysis of the dark spectrum fitting atmospheric correction for metre-and decametre-scale satellite imagery using autonomous hyperspectral radiometry,” Optics Express, 28(20), 29948-29965, https://doi.org/10.1364/OE.397456
TBD